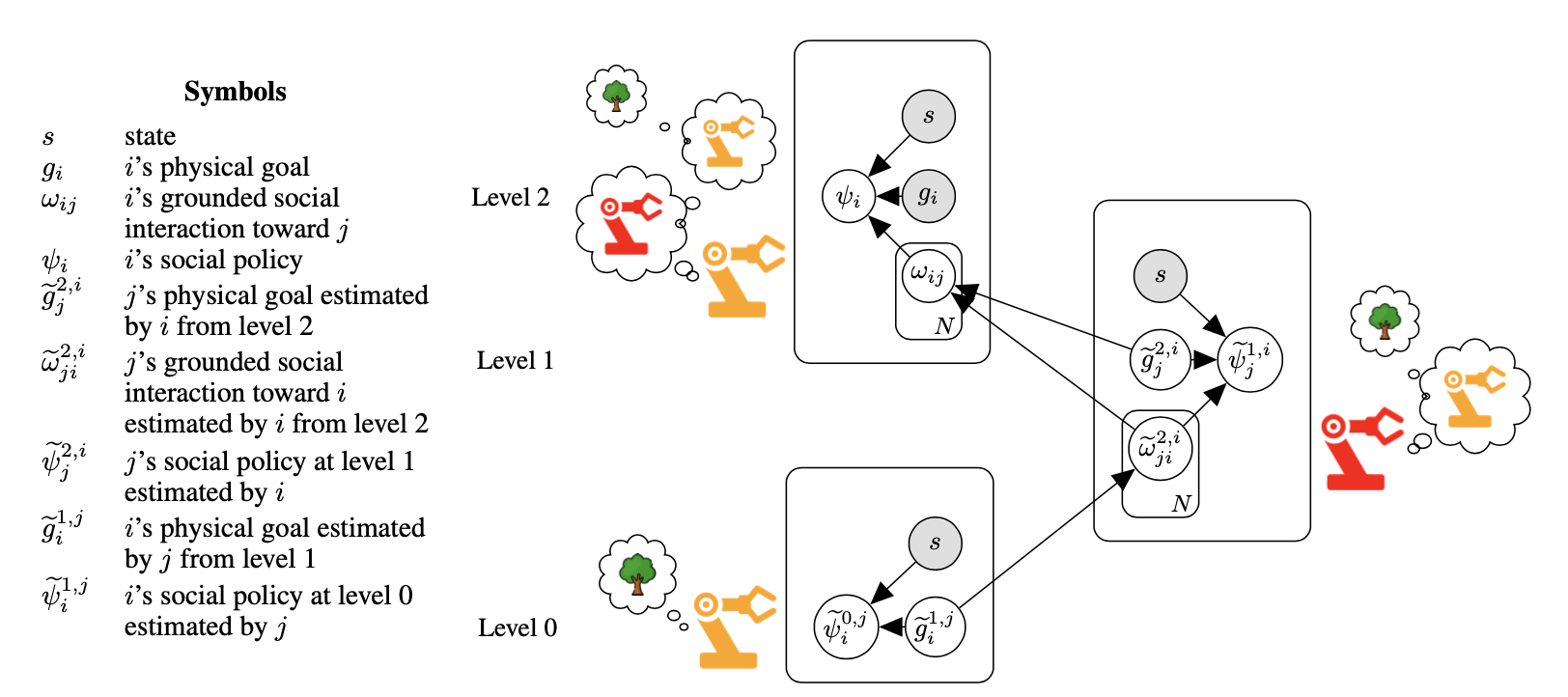
Linear Social MDP
How a robot responds socially, should depend on what it thinks the other robot is doing at that point in time. To encode this notion, we take linear combinations of social interactions as defined in Social MDPs, and compute the weights on those combinations on the fly depending on the goals of other robots. This new model, the Linear Social MDP, enables zero-shot reasoning about complex social interactions, provides a mathematical basis for the long-standing intuition that social interactions should compose, and leads to interesting new behaviors that we validate using human observers. Complex social interactions are part of the future of robotics, and having principled mathematical models built on a foundation like MDPs will make it possible to bring social interactions to every robotic application.
Scenarios
We use a two-agent (a yellow and red robot) 10x10 grid-world environment, with five actions (move in one of four directions or stay in place), three physical goals (watering the tree, adding logs to a fire and sawing logs), three locations (tree, fire, and saw), and two objects (a log, and a water can). In addition to the three physical goals, any combination of physical goals is possible, along with one of five social goals (cooperation, conflict, competition, coercion, or exchange) each related to one or more physical goals. Robots can move objects by pushing them.
In all experiments each robot always attempts to achieve two physical goals while engaging in social interactions relative to those goals. Those social interactions are conditioned on the physical goals of the other agent; or rather, on what the first agent thinks the second agent is doing. Despite having a fully-observable environment, agents do not have access to each other’s internal states and must estimate each other’s goals.
We explored every social scenario in this environment. The Yellow robot always had at most one social interaction, while the Red robot always had at most two social interactions. This resulted in 6x6x5 = 180 scenarios (eliminating the cause where neither agent considers any social interaction).
See list of all scenarios.
Results
Social Interactions conditioned over Physical goals
| Social Interaction | Human | Linear Social MDP | Inverse Planning | LSTM | ||||
|---|---|---|---|---|---|---|---|---|
| Physical Goal (Tree) | Physical Goal (Fire) | Physical Goal (Saw) | Physical Goal (Tree) | Physical Goal (Fire) | Physical Goal (Saw) | |||
| Cooperate | 0.821 | 0.783 | 0.792 | 0.772 | 0.752 | 0.759 | 0.742 | 0.521 |
| Conflict | 0.782 | 0.813 | 0.771 | 0.713 | 0.692 | 0.731 | 0.717 | 0.459 |
| Competition | 0.681 | 0.693 | 0.675 | 0.658 | 0.722 | 0.597 | 0.431 | 0.278 |
| Coercion | 0.827 | 0.787 | 0.812 | 0.804 | 0.755 | 0.793 | 0.323 | 0.172 |
| Exchange | 0.671 | 0.651 | 0.686 | 0.711 | 0.632 | 0.700 | 0.446 | 0.081 |
Overall
| Social Interaction | Human | Linear Social MDP | Inverse Planning | LSTM |
|---|---|---|---|---|
| Cooperation | 0.798 | 0.761 | 0.742 | 0.521 |
| Conflict | 0.788 | 0.712 | 0.717 | 0.459 |
| Competition | 0.683 | 0.659 | 0.431 | 0.278 |
| Coercion | 0.808 | 0.784 | 0.323 | 0.172 |
| Exchange | 0.669 | 0.681 | 0.446 | 0.081 |
Humans rated how well they could understand the social interactions produced by Linear Social MDPs. Chance is 20%, overall, they were able to recognize every social interaction, with "exchange" being the most difficult. Linear Social MDPs could recognize the resulting movies as well, while the inverse planning-based model and the LSTM had difficulty doing so.